A data set has values yi, each of which has an associated modelled value fi (also sometimes referred to as ŷi). Here, the values yi are called the observed values and the modelled values fi are sometimes called the predicted values.
The "variability" of the data set is measured through different sums of squares:
 the total sum of squares (proportional to the sample variance);
the total sum of squares (proportional to the sample variance);
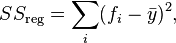 the regression sum of squares, also called the explained sum of squares.
the regression sum of squares, also called the explained sum of squares.
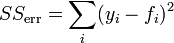 , the sum of squares of residuals, also called the residual sum of squares.
, the sum of squares of residuals, also called the residual sum of squares.
In the above  is the mean of the observed data:
is the mean of the observed data:
 is the mean of the observed data:
is the mean of the observed data:
where n is the number of observations.
The notations 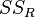 and
and  should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
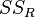 and
and  should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
The most general definition of the coefficient of determination is


No comments:
Post a Comment